EVALUACIÓN 1 PERIODO

1. ¿A qué se le denomina sistemas MKS?

A. METROS, KILOMETROS, SEGUNDOS.

B. METROS, KILOGRAMOS, SEGUNDOS.

C. YARDAS, CENTIMETROS, HORAS.

D. HECTAREAS, PULGDAS, PIES.

2. ¿Quiénes conforman el sistema inglés?

A. Las magnitudes.

B. El tiempo y la longitud.

C. Pies, kilos, segundos.

D. Las dimensiones métricas.

3. ¿Qué es una magnitud física?

A. Es una característica de un sistema inglés.

B. Es una característica de un sistema que se puede cuantificar o medir.

C. Es una forma de medición americano.

D. Es un proceso de dimensiones métricas.

4. ¿Qué es medición?

A. Es un proceso básico de la ciencia.

B. Es una magnitud física.

C. Es un periodo de tiempo.

D. Es una forma de cuantificación que pertenece al sistema inglés.

5. ¿Cuáles son los tipos de medición más utilizados?

A. METROS, KILOMETROS, SEGUNDOS.

B. METROS, KILOGRAMOS, SEGUNDOS.

C. HECTAREAS, PULGDAS, PIES.

D. Sistema inglés, sistema MKS y sistema CGS.

6. El movimiento de un cuerpo es:

A. Absoluto.

B. Relativo.

C. Absoluto y relativo.

D. Ni absoluto ni relativo.

7. Un cuerpo que se lanza verticalmente hacia arriba con una velocidad de 4.9m/s. dura en el aire:

A. 2 segundos.

B. O.5 segundos.

C. 0.25 segundos.

D. Ninguna de las anteriores.

8. Representa gráficamente si el siguiente ejercicio es de proporcionalidad directa o inversa:
entre más promociones más compras.

9. Los astronautas tienen menos masa en:

A. En la luna.

B. En la tierra.

C. Igual masa en la luna y en la tierra.

D. Las anteriores afirmaciones son falsas.

10. Representa gráficamente si el siguiente ejercicio es de proporcionalidad directa o inversa:
entre mas propagandas menos novelas.

EVALUACION 2 PERIODO

1. La aceleración gravitacional en la Luna es cerca de 1/6 de la aceleración en la Tierra. Si sobre la superficie de la Luna usted pudiera lanzar un balón hacia arriba con la misma velocidad que sobre la superficie de la Tierra, ¿Cuál de las siguientes afirmaciones sería correcta?

A. a. El balón tarda el mismo tiempo en alcanzar la máxima altura en la Luna que en la Tierra.
B. El balón tardaría seis veces más del tiempo en la Luna que el tiempo que tarda en la Tierra.
C. El balón tardaría seis veces más del tiempo en la Tierra que el tiempo que tarda en la Luna.
D. El balón tardaría 1/6 del tiempo en la Luna que el tiempo que tarda en la Tierra.

2. Un pesista levanta una masa m, ¿Cómo es la fuerza F que ejerce el pesista comparada con el peso que levanta?
A. F > mg
B. mg > F
C. F ≥ mg
D. F = mg

3. El mismo pesista levanta ahora la masa m desde la cintura hasta la altura de sus brazos extendidos, en total 120 cm, para lo cual realiza un impulso inicial de una vez y media la gravedad. Se puede afirmar que la fuerza F que debió realizar inicialmente para levantar la masa m se puede expresar mediante:

A. F > mg
B. F=mg
C. F ≥ mg
D. F < mg

4. Indique si las afirmaciones siguientes con respecto al movimiento parabolico de proyectiles son verdaderas o falsas
a)la rapidez varia linealmente con el tiempob)el proyectil cae librementec)la aceleracion del proyectil varia durante el movimientod)la rapidez disminuye cuando sube y aumenta cuando bajae)el movimiento es uniformemente variado

5. Se lanza un proyectil con una velocidad inicial de 200 m/s y una inclinación, sobre la horizontal, de 30°. Suponiendo despreciable la pérdida de velocidad con el aire, calcular:

¿Cuál es la altura máxima que alcanza la bala?.

a) 2.038,74 m

b) 8.556 m

c) 37,567m

¿A qué distancia del lanzamiento alcanza la altura máxima?.

a)7,233.44m

b) 1.732,05 m

c)4569,0m

¿A qué distancia del lanzamiento cae el proyectil?.

a)48.172m

b)76,3846m

c) 3.464,1 m

6. Se dispone de un cañón que forma un ángulo de 60° con la horizontal. El objetivo se encuentra en lo alto de una torre de 26 m de altura y a 200 m del cañón. Determinar:

¿Con qué velocidad debe salir el proyectil?.

a) 49,46 m/s

b) 069,37 s/m

c) 98,222 m/s

Con la misma velocidad inicial ¿desde que otra posición se podría haber disparado?.

a) 8m

b) 17 m

c)34m

Los enunciados que encuentra a continuación se refieren a la siguiente ilustración, de dos ruedas en movimiento circular y que están unidas por una banda. El radio de la circunferencia mayor es R₁ = 3R₂. Referida a los problemas del 13 al 23.

1 V_l 2

7. La velocidad lineal es:

a. Mayor en la circunferencia 1.

b. Mayor en la circunferencia 2.

c. Igual en la circunferencia 1 y 2.

d. No se sabe.

8. Podemos decir con seguridad que el numero de vueltas es equivalente a:

a. n₁ = 3n₂.

b. 3n₁ = n₂.

c. n₁ = n₂.

d. 3n₁ = 2n₂.

9. La relación de la frecuencia d la rueda l con relación a la rueda 2 es:

a. f₂ = f₁.

b. f₂ = 3f₁.

c. f₂ =

f₁.

d. f₂ = 2f₁.

10. El periodo de la rueda 2 será:

a. La tercera parte del periodo de la rueda 1.

b. El triple del periodo 1.

c. Igual al periodo 1.

d. Será mayor que el periodo 1.

MARCO TEÓRICO 2 PERIODO

Caída libre

En fisica, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del área, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquial mente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.

El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción des-aceleradora de la gravedad, como un disparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.

Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación ni de paracaidas durante un cierto trayecto.

Ecuación del movimiento

De acuerdo a la segunda ley de Newton, la fuerza

\mathbf{F}

que actúa sobre un cuerpo es igual al producto de su masa

m\,

por la aceleración que adquiere. En caída libre sólo intervienen el peso

\mathbf{P}

(vertical, hacia abajo) y el rozamiento aerodinámico

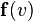\mathbf{f}(v)

en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:

$\mathbf{F} = \mathbf{P}+\mathbf{f} = -mg {\mathbf{j}} - f\frac{\mathbf{v}}{v} = m\frac{d\mathbf{v}}{dt}$

La aceleración de la gravedad

g\,

lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.

Trayectoria en caída libre

Caída libre totalmente vertical

El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la velocidad aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:

(1) $-mg + f = ma_y \,$

donde:

a_y, v_y\;

, son la aceleración y la velocidad verticales.

f\;

, es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).

Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuacion diferencial (1) para las velocidades y la altura vienen dada por:

$\begin{matrix} v_y(t)= v_0 - gt \\ y(t) = h_0 + v_0t -\frac{1}{2}gt^2 \end{matrix}$

donde v₀ es la velocidad inicial, para una caída desde el reposo v₀ = 0 y h₀ es la altura inicial de caída.

Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinamica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico k_w:

(2) $-mg - k_wv_y = ma_y \,$

En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial (2):

$\begin{cases} v_y = v_0e^{-k_wt/m} + \cfrac{mg}{k_w}(e^{-k_wt/m}-1) \\ y = h_0 - \cfrac{mgt}{k_w}+m\left(\cfrac{mg+k_wv_0}{k_w^2}\right)(e^{-k_wt/m}-1) \end{cases}$

No tese que en este caso existe una velocidad limite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:

$v_\infty = \lim_{t\to \infty} v_y(t) = -\frac{mg}{k_w}$

Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:

(3) $ma_y = m\frac{d^2y}{dt^2} = -mg - \epsilon\frac{C_d}{2}\rho A_tv_y^2$

Movimiento parabólico

Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.

En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales)..

Ecuaciones del movimiento parabólico

Hay dos ecuaciones que rigen el movimiento parabólico:

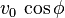$\mathbf{v_0} = v_0 \, \cos{\phi} \, \mathbf{i} + v_0 \, \sin{\phi} \, \mathbf{j}$
$\mathbf{a} = -g \, \mathbf{j}$

donde:

v_0 \,

es el módulo de la velocidad inicial.

\phi \,

es el ángulo de la velocidad inicial sobre la horizontal.

g \,

es la aceleración de la gravedad.

\mathbf{i}, \mathbf{j}

son dos versores (vectores unitarios) en el plano.

La velocidad inicial se compone de dos partes:

v_0 \, \cos{\phi}

que se denomina componente horizontal de la velocidad inicial.

En lo sucesivo

v_{0x} \,

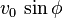v_0 \, \sin{\phi}

que se denomina componente vertical de la velocidad inicial.

En lo sucesivo

v_{0y} \,

Se puede expresar la velocidad inicial de este modo:

\mathbf{v_0} = v_{0x} \, \mathbf{i} + v_{0y} \, \mathbf{j}

: [ecu. 1]

Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.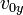

Ecuación de la aceleración

La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:

\mathbf{a} = -g \, \mathbf{j}

que es vertical y hacia abajo.

Ecuación de la velocidad

La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:

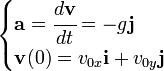
$\begin{cases} \mathbf{a} = \cfrac{d\mathbf{v}}{dt} = -g \mathbf{j} \\ \mathbf{v}(0) = v_{0x}\mathbf{i}+v_{0y}\mathbf{j} \end{cases}$

La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:

$\mathbf{v}(t) = v_{0x}\mathbf{i}+(v_{0y}-gt)\mathbf{j}$

Movimiento circular uniforme

En física, el movimiento circular uniforme (también denominado movimiento uniformemente circular) describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular.

Aunque la rapidez del objeto es constante, su velocidad no lo es: La velocidad, una magnitud vectorial, tangente a la trayectoria, en cada instante cambia de dirección. Esta circunstancia implica la existencia de una aceleración que, si bien en este caso no varía al módulo de la velocidad, sí varía su dirección.

Cinemática del MCU en mecánica clásica

Ángulo y velocidad angular

El ángulo abarcado en un movimiento circular es igual al cociente entre la longitud del arco de circunferencia recorrida y el radio.

La longitud del arco y el radio de la circunferencia son magnitudes de longitud, por lo que el desplazamiento angular es una magnitud adimensional, llamada radián. Un radián es un arco de circunferencia de longitud igual al radio de la circunferencia, y la circunferencia completa tiene

2\pi\,

radianes.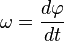

La velocidad angular es la variación del desplazamiento angular por unidad de tiempo:

$\omega = \frac{d\varphi}{dt}$

Partiendo de estos conceptos se estudian las condiciones del movimiento circular uniforme, en cuanto a su trayectoria y espacio recorrido, velocidad y aceleración, según el modelo físico cinemático.

Posición

Se considera un sistema de referencia en el plano xy, con vectores unitarios en la dirección de estos ejes

(\text{O}; \mathbf i, \mathbf j)

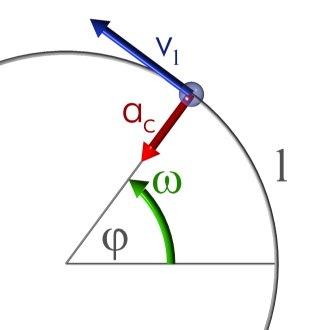
. La posición de la partícula en función del ángulo de giro

\varphi

y del radio r es en un sistema de referencia cartesiano xy:

$\begin{cases} x = r \cos \varphi \\ y = r \sin \varphi \end{cases}$

De modo que el vector de posición de la partícula en función del tiempo es:

\mathbf {r} = r \cos (\omega t) \mathbf i + r \sin (\omega t) \mathbf j

siendo:

\mathbf{r} \;

: es el vector de posición de la partícula.

r \;

: es el radio de la trayectoria.

Al ser un movimiento uniforme, a iguales incrementos de tiempo le corresponden iguales desplazamientos angulares, lo que se define como velocidad angular (ω):

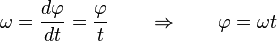
$\omega = \frac{d\varphi}{dt} = \frac{\varphi}{t} \qquad\Rightarrow\qquad \varphi = \omega {t}$

El ángulo (φ), debe medirse en radianes:

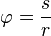
$\varphi = \frac{s}{r}$

donde s es la longitud del arco de circunferencia
Según esta definición:

1 vuelta = 360° = 2 π radianes

½ vuelta = 180° = π radianes
¼ de vuelta = 90° = π /2 radianes

Velocidad tangencial[editar]

La velocidad se obtiene a partir del vector de posición mediante derivación tangencial:

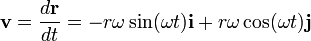
$\mathbf{v} = \frac{d\mathbf r}{dt} = -r\omega\sin (\omega t) \mathbf i + r\omega\cos (\omega t) \mathbf j$

La relación entre la velocidad angular y la velocidad tangencial es:

${v} = |\mathbf v | = \sqrt {(-r\omega\sin (\omega t))^2 + (r\omega\cos (\omega t))^2} = \omega r$

El vector velocidad es tangente a la trayectoria, lo que puede comprobarse fácilmente efectuando el producto escalar

\mathbf r \cdot \mathbf v

y comprobando que es nulo.

Aceleración

La aceleración se obtiene a partir del vector velocidad con la derivación:

$\mathbf{a} = \frac{d\mathbf v}{dt} = -r\omega^2\cos (\omega t) \mathbf i - r\omega^2\sin (\omega t) \mathbf j$

de modo que

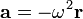
$\mathbf{a} = -\omega^2 \mathbf r$

Así pues, el vector aceleración tiene dirección opuesta al vector de posición, normal a la trayectoria y apuntando siempre hacia el centro de la trayectoria circular. por lo que acostumbramos a referirnos a ella como aceleración normal o centrípeta.

El módulo de la aceleración es el cuadrado de la velocidad angular por el radio de giro, aunque lo podemos expresar también en función de la celeridad

v\,

de la partícula, ya que, en virtud de la relación

v=\omega r\,

, resulta

$a = \omega^2 r = \frac{v^2}{r}$

Esta aceleración es la única que experimenta la partícula cuando se mueve con rapidez constante en una trayectoria circular, por lo que la partícula deberá ser atraída hacia el centro mediante una fuerza centrípeta que la aparte de una trayectoria rectilínea, como correspondería por la ley de inercia.

fisica

miércoles, 19 de marzo de 2014

EVALUACION FISICA!!!!

LABORATORIOS

ENTRETENIMIENTO

MARCO TEÓRICO